9 Billion Divided By 4 Million
hodlers
Dec 06, 2025 · 13 min read
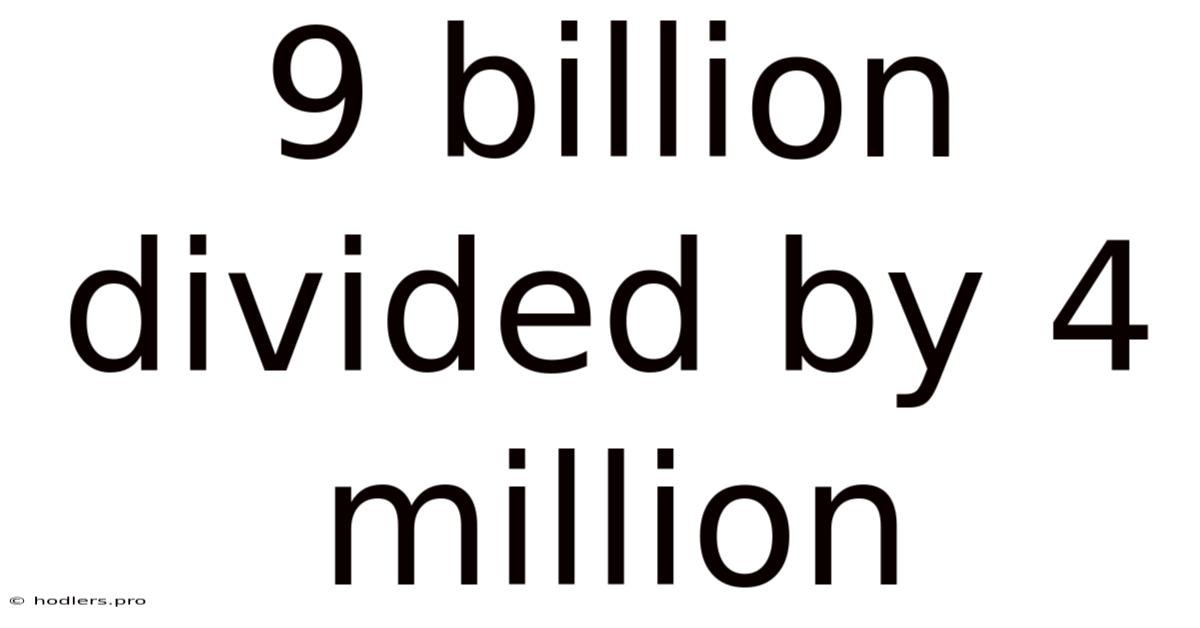
Table of Contents
Imagine you're responsible for distributing resources – food, medicine, or even financial aid – to a large population. You have a total of nine billion units of this resource and need to ensure it's divided fairly among four million people. How do you determine how much each person receives? This scenario, though simplified, perfectly illustrates the importance of understanding division, especially when dealing with large numbers. The calculation of 9 billion divided by 4 million isn't just a mathematical exercise; it’s a fundamental operation with real-world applications across various fields.
Understanding the concept of division allows us to tackle problems related to resource allocation, data analysis, and financial planning. In its simplest form, division helps us break down a large quantity into smaller, equal parts. In the case of 9 billion divided by 4 million, we are essentially determining how many units are in each of those smaller parts. This mathematical operation is not limited to theoretical applications; it plays a crucial role in our daily lives, from calculating the cost per item when buying in bulk to understanding statistical data presented in millions or billions. By exploring this specific calculation, we can gain a better appreciation for the power and utility of division in making sense of the world around us.
Understanding the Basics of Division
At its core, division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. The act of dividing helps us to understand how many times one number (the divisor) is contained within another number (the dividend). The result of this process is called the quotient. In our specific example, 9 billion divided by 4 million, 9 billion is the dividend, 4 million is the divisor, and the result we seek is the quotient.
To delve deeper, it's important to understand the terminology. The dividend is the number that is being divided, the divisor is the number by which the dividend is being divided, and the quotient is the result of the division. There can sometimes be a remainder, which is the amount left over when the dividend cannot be divided evenly by the divisor. For instance, if you were to divide 10 by 3, you would get a quotient of 3 and a remainder of 1, because 3 goes into 10 three times with 1 left over. This basic understanding sets the stage for comprehending more complex divisions, especially those involving large numbers like billions and millions.
Division is also intrinsically linked to multiplication. Division can be seen as the inverse operation of multiplication. This means that if you divide a number by another, you can check your answer by multiplying the quotient by the divisor. If the result equals the dividend, the division was performed correctly. For example, if 9 billion divided by 4 million equals 2250, then 2250 multiplied by 4 million should equal 9 billion. This inverse relationship provides a simple yet effective method for verifying the accuracy of division calculations, especially when dealing with numbers that are difficult to manage mentally.
Historically, the concept of division has evolved over centuries. Ancient civilizations, including the Egyptians and Babylonians, developed their own methods for performing division, often using tables and algorithms to simplify the process. The modern division symbol (÷) and the long division method we commonly use today are relatively recent developments, but they build upon the foundational understanding of division that has been cultivated for thousands of years. Understanding the historical context of division highlights its enduring importance as a fundamental mathematical operation.
Scientifically, division is not merely a mathematical construct but a fundamental aspect of how we understand and model the world. In physics, division is used to calculate speed (distance divided by time) and density (mass divided by volume). In chemistry, it helps determine concentrations (amount of solute divided by volume of solution). Even in computer science, division is a basic operation used in algorithms for data processing and analysis. The widespread application of division across scientific disciplines underscores its practical utility beyond simple arithmetic.
The Calculation: 9 Billion Divided by 4 Million
Now, let's perform the division of 9 billion divided by 4 million. Writing this out mathematically, we have 9,000,000,000 ÷ 4,000,000. One of the first steps to simplify this calculation is to recognize that both numbers have several trailing zeros. We can simplify the calculation by canceling out the common zeros in both the dividend and the divisor. In this case, both 9 billion and 4 million have six trailing zeros, which can be eliminated.
After canceling out the six zeros from both numbers, we are left with 9,000 ÷ 4. This simplification makes the division much easier to manage. Now, we can perform this division using long division or a calculator. Dividing 9,000 by 4 gives us a result of 2,250. Therefore, 9 billion divided by 4 million equals 2,250.
This result, 2,250, can be interpreted in various ways depending on the context. For example, if we were distributing 9 billion dollars among 4 million people, each person would receive $2,250. Alternatively, if we were dividing 9 billion units of a product among 4 million stores, each store would receive 2,250 units. Understanding the context is crucial for interpreting the result of the division accurately and applying it effectively.
It's also helpful to verify the result to ensure accuracy. As mentioned earlier, we can check the division by multiplying the quotient (2,250) by the divisor (4 million). If the result equals the dividend (9 billion), then our calculation is correct. Multiplying 2,250 by 4,000,000 indeed equals 9,000,000,000, confirming that our division is accurate. This verification step is essential in any mathematical calculation, especially when dealing with large numbers.
Another way to conceptualize this division is to think of it in terms of ratios or proportions. The ratio of 9 billion to 4 million is equivalent to the ratio of 2,250 to 1. This means that for every 1 unit of the divisor (4 million), there are 2,250 units of the dividend (9 billion). Understanding this proportional relationship can be helpful in various applications, such as scaling recipes or converting units of measurement.
Trends and Applications in Real-World Scenarios
The simple calculation of 9 billion divided by 4 million has surprisingly diverse applications in various fields. In economics, for example, it can be used to calculate per capita income or to analyze the distribution of wealth. Governments and international organizations often use such divisions to understand how resources are allocated across populations. Consider a scenario where a country's GDP is 9 billion dollars and its population is 4 million. Dividing the GDP by the population gives us the per capita income, which provides a measure of the average income per person in that country.
In business and finance, this type of calculation is crucial for analyzing market size, calculating market share, and determining investment returns. For instance, if a company has total sales of 9 billion dollars and serves a market of 4 million customers, dividing the total sales by the number of customers can give the average revenue per customer. This metric can then be used to assess customer value and inform marketing strategies.
Healthcare is another area where such divisions are relevant. Public health organizations might use this calculation to determine the allocation of medical resources or to analyze disease prevalence rates. For example, if there are 9 billion doses of a vaccine available for a population of 4 million people, dividing the total doses by the population size can help determine how many doses are available per person, aiding in vaccination planning and distribution.
Recent trends in data analysis and big data have further amplified the importance of performing divisions with large numbers. With the increasing availability of data in millions and billions, the ability to quickly and accurately perform these calculations is essential for extracting meaningful insights and making informed decisions. Data scientists and analysts frequently use such divisions to normalize data, calculate rates and ratios, and perform statistical analyses.
However, it's important to be aware of potential pitfalls when working with large numbers. One common mistake is to misplace or miscount zeros, which can lead to significant errors in the calculation. Another challenge is dealing with rounding errors, especially when using calculators or computers. Rounding errors can accumulate and distort the final result, particularly in complex calculations involving multiple steps. Therefore, it's essential to use appropriate precision and to verify the results whenever possible.
Another trend is the increasing reliance on automation and software tools for performing these calculations. Spreadsheets, statistical software packages, and programming languages provide efficient and accurate ways to divide large numbers and perform more complex mathematical operations. These tools not only reduce the risk of human error but also allow for more sophisticated analyses and simulations.
Practical Tips and Expert Advice
When performing division, especially with large numbers like 9 billion divided by 4 million, accuracy and efficiency are key. Here are some practical tips and expert advice to ensure your calculations are correct and meaningful:
-
Simplify the numbers: As demonstrated earlier, canceling out common zeros in both the dividend and the divisor can significantly simplify the calculation. This reduces the risk of making mistakes and makes the division easier to manage mentally or with a calculator.
-
Use a calculator or spreadsheet: While it's good to understand the underlying principles of division, using a calculator or spreadsheet can help ensure accuracy and speed, especially when dealing with large numbers. Tools like Microsoft Excel, Google Sheets, and online calculators are readily available and can perform complex divisions with ease.
-
Double-check your work: Always verify your results to ensure they are accurate. As mentioned earlier, you can check the division by multiplying the quotient by the divisor to see if it equals the dividend. If there's a discrepancy, review your steps and recalculate.
-
Understand the context: The result of a division is only meaningful if you understand the context in which it is being applied. Consider what the numbers represent and how the division relates to the problem you are trying to solve. This will help you interpret the result accurately and draw meaningful conclusions.
-
Pay attention to units: When working with real-world data, make sure to pay attention to the units of measurement. For example, if you are dividing dollars by people, the result will be dollars per person. Including the units in your calculations and results will help prevent confusion and ensure that your analysis is accurate.
-
Break down complex problems: If you are faced with a complex problem that involves multiple divisions or other mathematical operations, break it down into smaller, more manageable steps. This will make the problem easier to understand and solve, and reduce the risk of making mistakes.
-
Use estimation: Before performing the division, try to estimate the result. This can help you identify potential errors and ensure that your final answer is reasonable. For example, you might estimate that 9 billion divided by 4 million is approximately 2,000, which is close to the actual result of 2,250.
-
Be mindful of rounding errors: When using calculators or computers, be aware of potential rounding errors. Use appropriate precision and consider rounding the final result to a reasonable number of decimal places. Avoid excessive rounding, as this can distort the accuracy of your results.
-
Practice regularly: Like any skill, performing division accurately and efficiently requires practice. Regularly work through examples and problems to improve your understanding and build your confidence.
By following these tips and seeking expert advice when needed, you can confidently perform division with large numbers and apply the results effectively in various real-world scenarios.
FAQ: Dividing Large Numbers
Q: How do I divide 9 billion by 4 million without a calculator? A: Simplify by canceling common zeros. 9,000,000,000 ÷ 4,000,000 becomes 9,000 ÷ 4. Then, use long division.
Q: What is the significance of the result when dividing 9 billion by 4 million? A: The result, 2,250, represents the quantity each of the 4 million parts would receive if 9 billion was divided equally among them. The significance depends on the context; it could be dollars per person, units per store, etc.
Q: Can I use a spreadsheet program like Excel to perform this calculation? A: Yes, spreadsheet programs are ideal for this. Simply enter "=9000000000/4000000" into a cell, and it will display the result.
Q: What are some common mistakes to avoid when dividing large numbers? A: Common mistakes include miscounting zeros, incorrect placement of the decimal point, and rounding errors. Always double-check your work and use a calculator or spreadsheet for accuracy.
Q: How does this calculation relate to real-world applications? A: It relates to many areas, including economics (per capita income), business (market share), and healthcare (resource allocation).
Q: Why is it important to understand the context when interpreting the result of a division? A: Context provides meaning. 2,250 could be dollars, units, or some other measure. Understanding the context ensures you interpret the result accurately and make informed decisions.
Q: Is there a way to estimate the answer before performing the actual division? A: Yes, you can round the numbers to make the division easier. For example, round 9 billion to 10 billion and 4 million to 5 million. Then, 10 billion ÷ 5 million = 2,000, which is a reasonable estimate.
Q: How can I ensure the accuracy of my division calculations? A: Use a calculator or spreadsheet, double-check your work, and understand the context of the problem. Also, be mindful of potential rounding errors.
Q: What if the numbers were not exact? For example, 9.1 billion divided by 3.8 million? A: The process is the same, but you'll likely need a calculator for accuracy. The result will be a decimal number, reflecting the more precise division.
Q: Can division problems like this be used in statistical analysis? A: Yes, absolutely. They are often used to calculate rates, ratios, and normalize data in statistical analysis.
Conclusion
The exercise of dividing 9 billion by 4 million demonstrates the fundamental importance of division in both mathematics and real-world applications. The result, 2,250, represents the quotient of this operation, but its true value lies in its interpretation within a specific context, be it economics, business, or healthcare. Mastering the art of division, particularly with large numbers, involves not only understanding the mechanics of the operation but also recognizing potential pitfalls, such as miscounting zeros or rounding errors, and employing strategies to mitigate them.
By simplifying numbers, utilizing tools like calculators and spreadsheets, and consistently verifying results, we can ensure the accuracy and reliability of our calculations. Moreover, understanding the context in which division is applied is crucial for interpreting the results meaningfully and making informed decisions. As we navigate an increasingly data-rich world, the ability to perform and interpret division accurately becomes ever more essential.
Now that you've grasped the intricacies of this division, we encourage you to apply this knowledge to real-world scenarios you encounter daily. Whether it's calculating your share of a group bill, understanding statistical data presented in millions or billions, or analyzing financial reports, the principles of division will empower you to make sense of the world around you. Share this article with your friends and colleagues, and let's collectively enhance our understanding and application of this fundamental mathematical operation. What are some creative ways you can apply this calculation in your field or daily life? Share your thoughts and insights in the comments below!
Latest Posts
Related Post
Thank you for visiting our website which covers about 9 Billion Divided By 4 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.